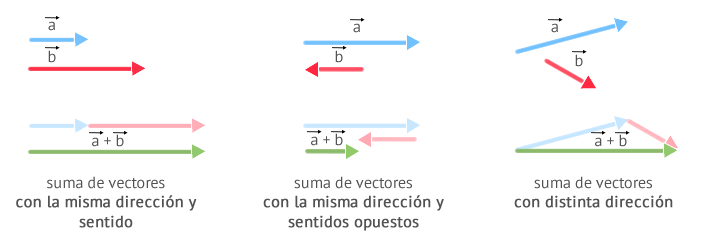
¿Qué es la Adición de Vectores?

La adición de dos matrices A + B  requiere que las matrices sean de dimensiones iguales. A continuación cada elemento de una matriz se suma, del elemento correspondiente de la otra matriz. Es decir lo único que tenemos que hacer es sumar las respectivas componentes de los vectores sumandos, obteniendo así, el vector suma.

¿Cómo se Gráfica? 

Mediante 2 métodos distintos: el método de la cabeza con cola (o del extremo con origen) y la regla del paralelogramo.

Método de la cabeza con Cola

Respetando la dirección y sentido de ambos vectores.

1. Desplazamos el Vector b de tal forma que su origen se encuentre a continuación del extremo del Vector a
2. El Vector C será el segmento recto que podamos dibujar desde el origen de a hasta el origen de b

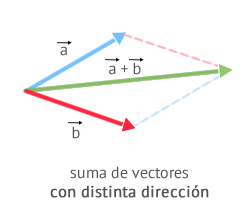
Regla del Paralelogramo

La podemos aplicar si los vectores no tienen la misma dirección:

1. Se sitúan los Vectores a y b con los orígenes en el mismo punto.
2. Desde el extremo de cada uno se dibuja una paralela al otro vector. Al final podremos ver un paralelogramo.
3. El Vector C  será el vector que parte desde el origen común de a y b a través de la diagonal del paralelogramo.

¿Cómo se representa Geométricamente un Vector Suma y Resta en un Sistema de Coordenadas en R3?  

Los vectores W y V sustentan un paralelogramo, el de la diagonal mayor es el vector suma y el vector de la diagonal menor es el vector diferencia. Es decir se representa con un Paralelogramo.

      

¿Qué es la Sustracción de Vectores?

Restar el vector B del vector A es equivalente a sumarle el inverso aditivo de B. Para restar vectores se unen en su origen y el vector resta es la unión de sus extremos dibujando el sentido hacia el que se le va a quitar, el paso siguiente es calcular el vector con el mismo procedimiento que en la suma.

¿Cómo se Gráfica?

El procedimiento general para restar vectores en forma gráfica es: 

1) Dibujar el primer vector. 

2) Dibuja el inverso del segundo vector. 

3) la resta va desde donde comienza el primer vector hasta donde termina el inverso del segundo vector.   

Deberás tener en cuenta que es lo que se llama el "Inverso de un Vector"

• Es un vector trazado sobre la misma linea de acción original.
• Tiene el mismo modulo que el vector original. 
• Va en dirección opuesta al vector dado originalmente.

Calculo de la Dirección de un Vector en R3

Calculo del Sentido de un Vector en R3 

El sentido de un Vector lo define la flecha dibujada sobre el segmento de recta. También podemos definir que el sentido de un vector en R3 es según la cantidad de Positivos y Negativos que se le asignen a dicho vector.